Jun 14, 2023 5 min read Split Testing

Visualizing Split-Test Parameters

In my previous blog post, I discussed the importance of selecting an appropriate sample size when running a split test. Selecting an appropriate sample size helps to ensure that you are making unbiased decisions within the error bounds you are comfortable with. However, this requires an understanding of split testing parameters. Although the definitions may suffice, visualizing the split test parameters can help solidify your understanding.

For this example, let's assume that we are trying to optimize the conversion rate of a sales funnel. We will refer to our existing sales funnel as A and the changes we are split testing as B. We will use the following values for our split test parameters:

Significance (α): 5%
Statistical Power (1-β): 80%
Minimum Detectable Effect (MDE): 5%
Conversion Rate (pA): 20%

Binomial Distribution

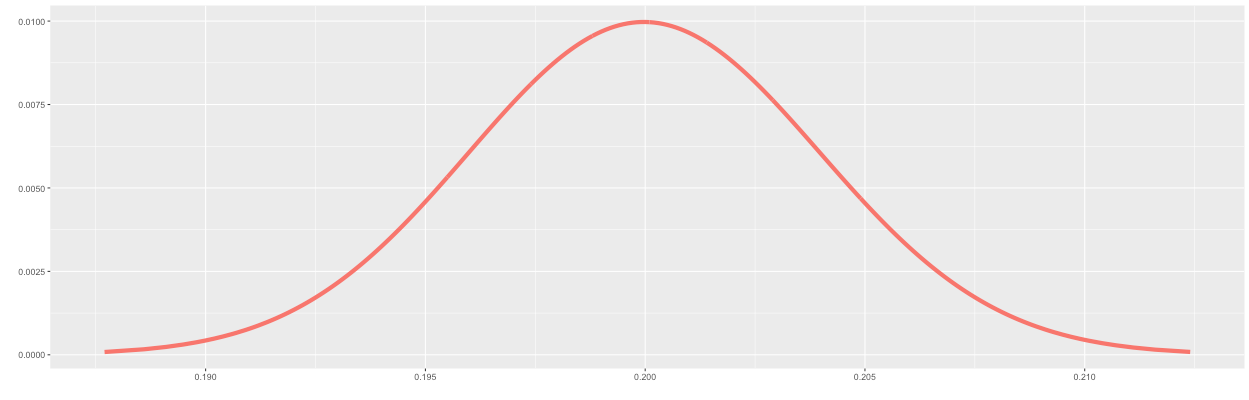
We will model the conversion rates of A and B using the binomial distribution. The binomial distribution takes two parameters: the number of trials (n) and the probability of success (p) and provides a distribution of the number of successes. By dividing the number of successes by n, we get a distribution of the conversion rate. When drawing the distribution for the conversion rate of A, we will set p equal to the conversion rate of 20% (pA=0.2). For now, we will use an arbitrary value of 10,000 for n. As expected, Figure 1 shows a distribution centered around 0.2.

Figure 1: Distribution of A (n=10000, pA=0.2)

When drawing the distribution of B, we will use the probability of A plus the minimum detectable effect of 5%. So pB = pA * (1 + MDE) = 0.21. As expected, Figure 2 shows one distribution for A centered around 0.2 and one distribution for B centered around 0.21.

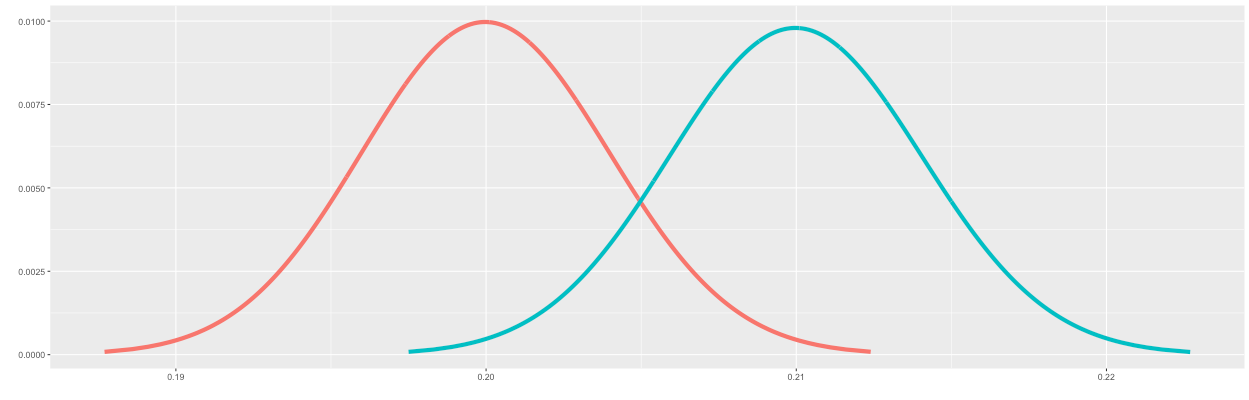
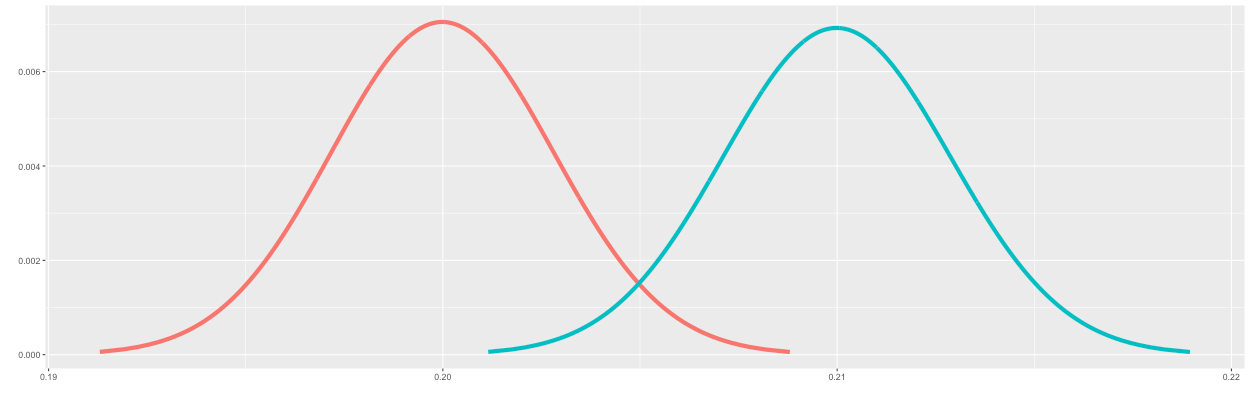
Figure 2: Distributions of A and B (n=10000, pA=0.2, pB=0.21)

You can see in Figure 2 that the two distributions overlap by some amount. The overlap between the two distributions decreases when the sample size (n) increases. In Figure 3, the sample size has been increased to 20,000. This is effectively what we are doing when selecting the sample size: controlling the outcomes of A and B such that it fits our split test parameters. You will see more on that later.

Figure 3: Distributions of A and B (n=20000, pA=0.2, pB=0.21)

Arcsine Transformation

Fitting the split test parameters to the distributions involves percentiles, so we must first convert our binomial distributions to normal distributions. By using the arcsine transform, we can model the conversion rate of A as a standard normal distribution (mean=0, sd=1) and the conversion rate of B as a normal distribution (mean=h*sqrt(n/2), sd=1). You may recall from my previous blog post that h is the effect size and is equal to 2*asin(sqrt(pB))-2*asin(sqrt(pA)).

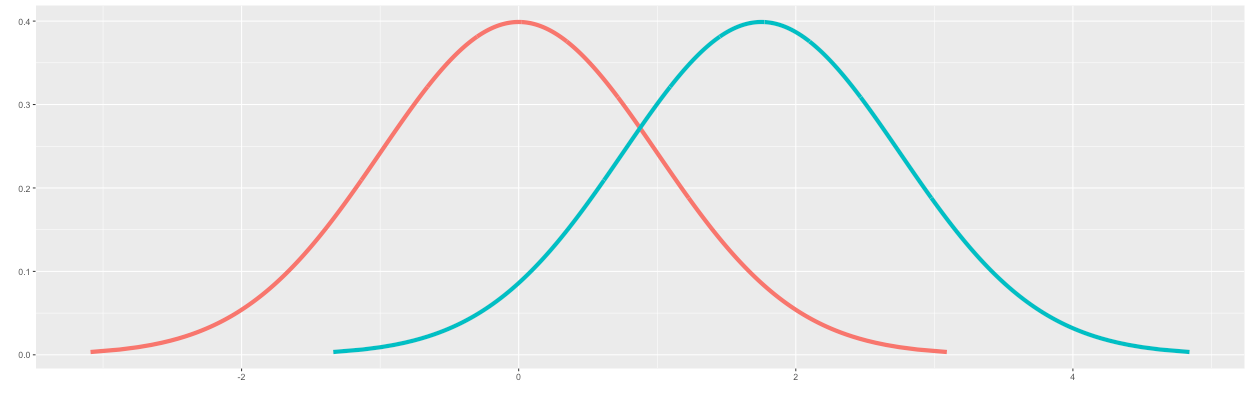
Figure 4: Normalized Distributions of A and B (n=10000, pA=0.2, pB=0.21)

Figure 4 shows the result of converting the binomial distributions into normal distributions. You will notice that the x-axis now corresponds to z-values instead of possible conversion rates.

Drawing the Parameters

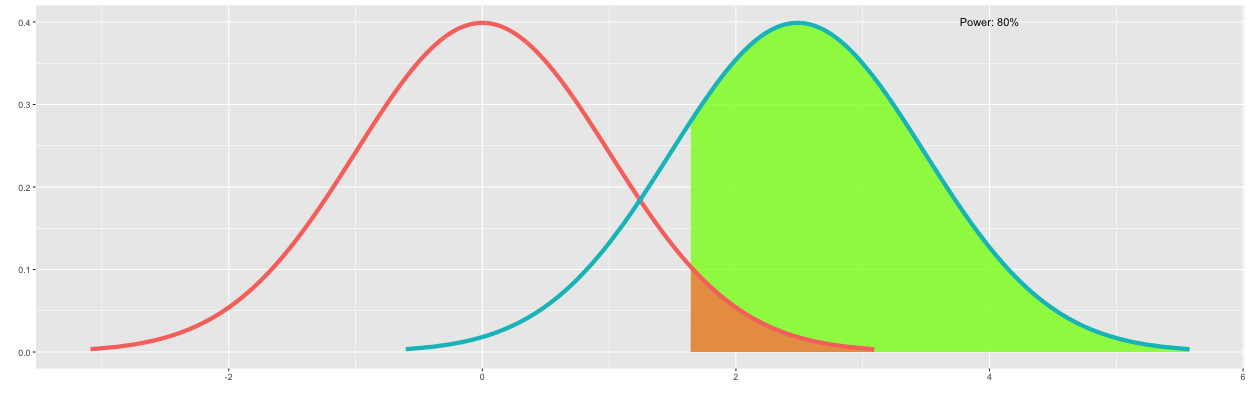
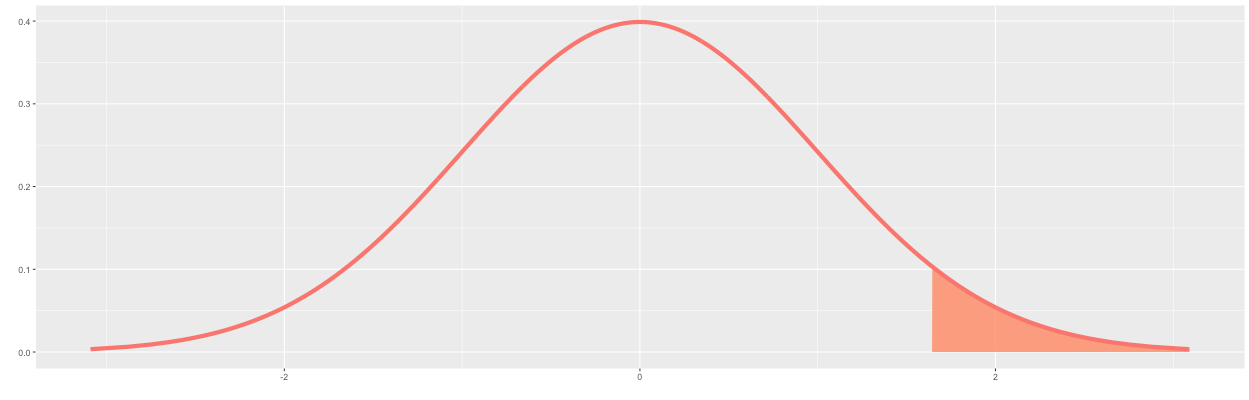
I will first draw the parameters for the alternative hypothesis in which the conversion rate of B is "greater" than A. We will first draw the significance level on the distribution of A. A significance level of 5% corresponds to the 95th percentile on the distribution of A (i.e., 1-0.05=0.95). This corresponds to a z of about 1.64, as shown in Figure 5 below.

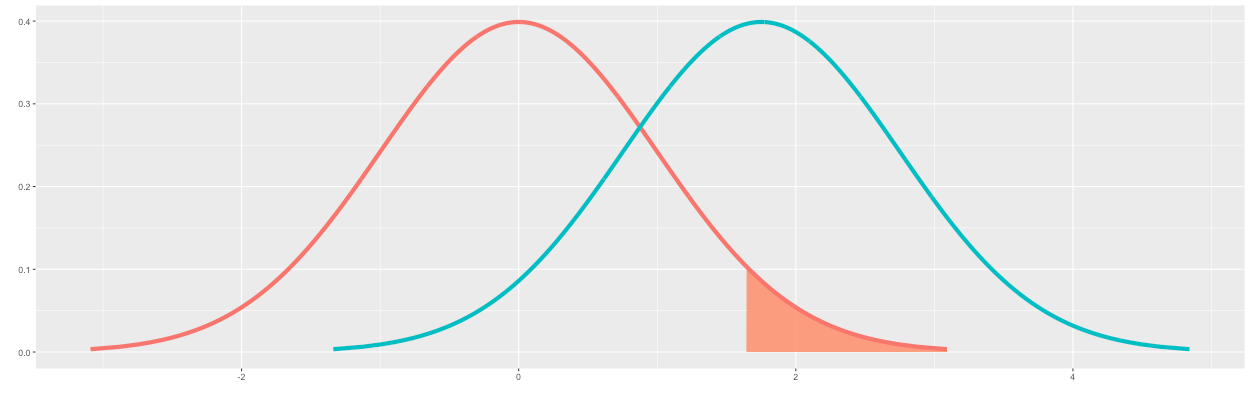
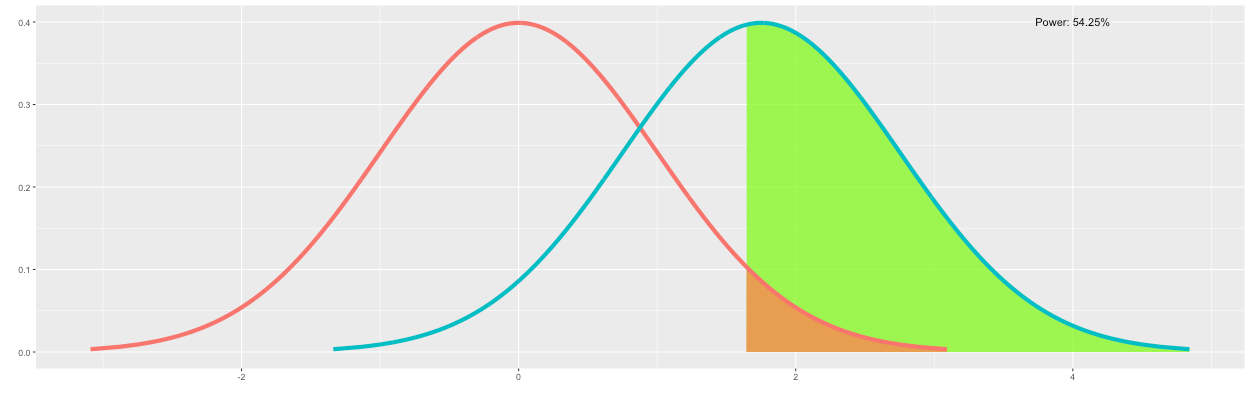
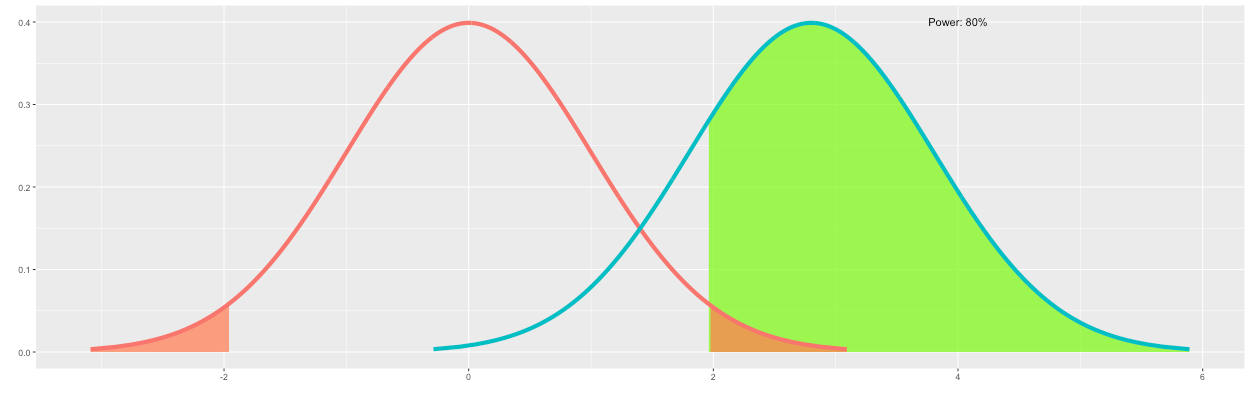
Figure 5: Drawing the Significance Level (pA > 0.95)

We can declare that the conversion rate of B is "greater" than A for outcomes of B to the right of the significance level. Because these are desired outcomes of B, I have colored this region green. Note that this percentile corresponds to the statistical power. As shown in Figure 6, the statistical power is approximately 54.25%.

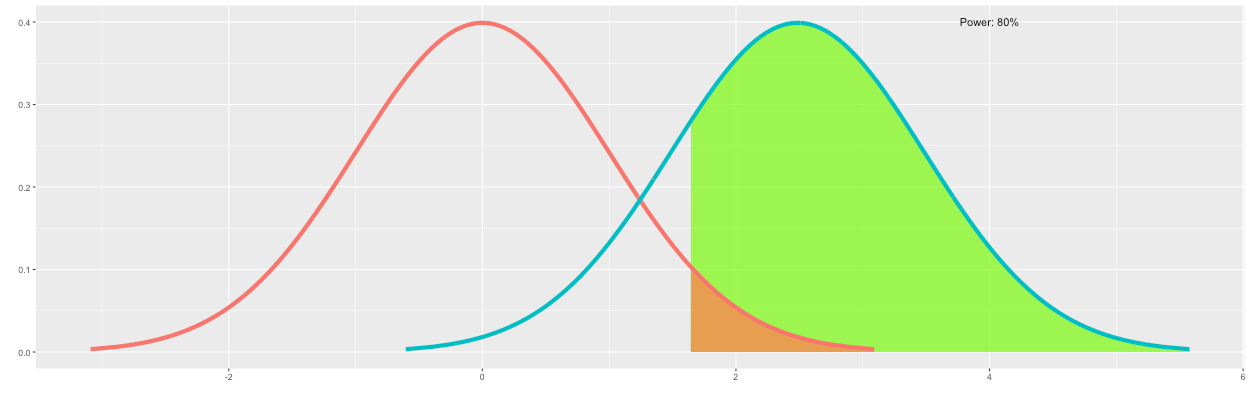
Figure 6: Drawing the Statistical Power (zB > 1.64, n=10000)

However, the desired statistical power is 80%. Therefore, we continue increasing n until 80% of the outcomes of B are to the right of the significance level. As shown in Figure 7, increasing n to 20,150 satisfies this requirement.

Figure 7: Finding the Required Sample Size (n=20150)

False Positives

You might be wondering why I colored the significance level red. This is because the significance level corresponds to the false positive rate. When determining the sample size, we assumed that the conversion rate of B is equal to the conversion rate of A plus the minimum detectable effect. However, let's now assume that the conversion rate of B is equal to the conversion rate of A. This is more difficult to visualize because the distributions of A and B would be stacked on top of each other, as shown in Figure 8. However, keep in mind that we can declare that the conversion rate of B is "greater" than A for outcomes to the right of the significance level. This explains why false positives are possible.

Two-Sided Tests

As you might expect, when the alternative hypothesis is "less," the required sample size is the same. However, for "two-sided" tests, the required sample size is larger. A "two-sided" test means testing if the conversion rate of B is greater than A or the conversation rate of B is less than A. The required sample size is larger because the significance is divided between each tail, as shown in Figure 9. Note that Figure 9 only shows the case where the conversion rate of B is greater than A. Intuitively this makes sense because the significance level is pushed further to the right, which requires a larger sample size to achieve the same statistical power.

Final Thoughts

In this post, I have demonstrated how to visualize split test parameters. If you want to explore this topic further, I recommend checking out my Sample Size Visualization Tool, which I used to generate the plots for this blog post. You can also find the source code here.